|
摘要 对激光陀螺速率捷联系统作为制导系统的惯性测量设备进行了研究,对其数学平台的解算进行了数值仿真,并对制导方程采用显式形式进行了研究和数值仿真,对速率捷联显式制导系统的方法误差、工具误差、综合误差进行了分析和计算,得出了可供设计参考的结论。
主题词 激光陀螺,捷联系统,显式制导,入轨精度。
The Research for the Laser Gyro Strapdown Explicit Guidance System
Zhou Manjuan
(Shanghai Institute of Mechanical and Electronic Equipment,Shanghai,201108)
Abstract Using laser gyro rate strapdown system as inertial measurement equipment of guidance system is researched.Arithmetic of its mathematical platform is numerical simulated.Guidance equation is studied and explicit numerical simulated.Methodical error,instrument error and composite error of rate strapdown explicit guidance system is analysied and calculated.The useful result for designing and reference is got.
Key Words Laser gyro,Strapdown system,Explicit guidance,Orbit injection accuracy.
1 前 言
激光陀螺具有精度高、测量范围宽、内部没有活动部件、受力学环境影响小、寿命长等特点,它是捷联系统的理想测量器件,因而得到了广泛的应用,美国、法国、日本等国都将激光陀螺捷联系统应用于火箭上。显式制导则是在飞行过程中,不断地计算火箭的实时速度和位置,利用实时速度、位置进行火箭制导方程的运算,以控制火箭沿标准弹道飞行,将载荷送入预定的轨道。过去由于箭机运算速度的限制,无法精确计算火箭的实时速度和位置,只能用视速度、视位置进行制导方程计算,将大量的数据处理工作放在地面进行,给设计和事后报轨带来大量的工作,采用显式制导后,则可简化设计和进行快速报轨。本文从硬件和软件两方面对制导系统进行了研究。
2 激光陀螺的原理
激光陀螺是利用环形腔内运行着的逆、顺时针的两束光进行转动载体的角速度测量的。当载体在惯性空间以某一角速度转动时,则这两束光的谐振频率之差也随载体角速度成正比变化。所以通过对拍频的测量,可以得到载体的角速度和转角。因此我们可以得到如下的表达式:
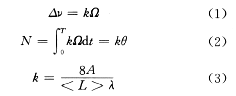
式中 Δν为拍频;k为比例因子;Ω为转动角速度;A为环形谐振腔面积;<L>为环形谐振腔环路长度;λ为激光波长。??
激光陀螺的输出脉冲频率正比于Ω,输出脉冲数正比于θ,利用该输出脉冲数可求出载体的角增量,从而可进行数学平台的解算。
3 激光陀螺捷联系统的组成及其数学平台
3.1
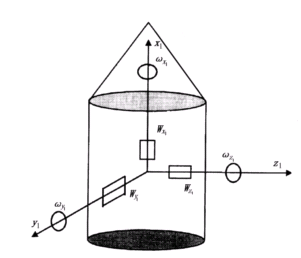
图1 激光陀螺速率捷联系统示意图
由3个激光陀螺和3个石英加速度计固连于运载火箭3个箭体轴上而成的捷联系统,如图1所示,3个激光陀螺测量沿箭体轴??x1,y1,z1方向的角速度ωx1,ωy1??,ωz1。3个加速度计测量沿箭体轴x1,y1,z1方向的视加速度Wx1, Wy1,Wz1。
3.2 数学平台
3.2.1 四元数运动学方程
在工程实际中,特别是用数值法解运动学方程时,四元数运动学方程得到了广泛的应用,这是因为四元数运动学方程对任何参数值都不退化(无奇点),而且参数数目少(只有4个),联系式数目最少(只有1个,即 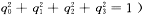 。假设运载火箭的角运动是刚体角运动,可得四元数运动学方程: 。假设运载火箭的角运动是刚体角运动,可得四元数运动学方程:
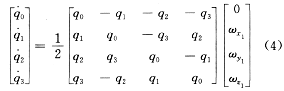
在ωx1,ωy1,ωz1已知的情况下,由式(4)进行差分法计算可解算出q0,q1,q2,q3。??
3.2.2 四元数变换
设A为箭体坐标系到惯性坐标系的转换矩阵,则有
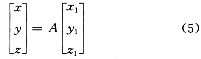
式中
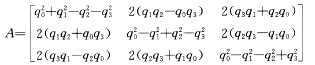
A?Ъ次?所说的由箭体到惯性系的数学平台转换矩阵,它是通过解算四元数运动方程而得到的。
3.3 四元数方程的解算
由式(4)用数值迭代法可解算出q0,q1,q2,q3。捷联系统中激光陀螺输出脉冲数代表箭体在采样时间内的转角增量,若已知箭体的初始转动四元数,并测得各采样时刻箭体的转角增量,则可用下述的一种数值迭代法求解四元数微分方程。
设陀螺仪测出箭体从第(k-1)次采样时间到第k?Т尾裳?时间内的转角增量为
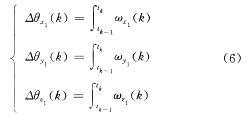
式中 Δθx1(k),Δθy1(k),Δθz1(k)分别为从第k-1次到第k次采样时间内箭体绕3个坐标轴的转角增量;tk-1为第k-1次采样时的时间;tk为第k次采样时的时间(k=1,2,3, …)?А*?
从第k-1次到第k次采样时间内,箭体转角增量的模为
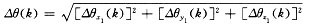
则四元数的差分解为:
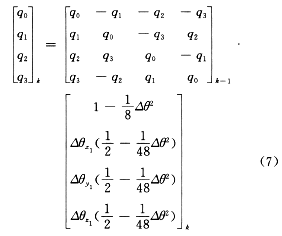
3.4 四元数的初值
按式(7)求解转动四元数时,需要知道第1次采样时刻(k=1)的初始四元数q(0),通常q(0)值可在箭体进行初始对准时求得。选用运载火箭起飞时刻发射点的惯性坐标系作为导航坐标系oxyz,且箭体坐标系ox1y1z1相对导航坐标系的初始不对准角度以图2所示的克雷洛夫角表示。按图2所示,箭体坐标系相对导航坐标系的初始位置可由与克雷洛夫角转动顺序有关的四元数表示,这些四元数可写为
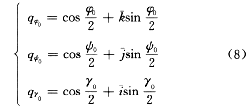
克雷洛夫角的转动顺序为φ0→ψ0→γ0,因此可得合成转动四元数q(0)=qφ0qψ0qγ0。?И?
将式(8)代入上式,并按四元数乘法规则展开,可得出以矩阵形式给出火箭起飞时的初始四元数为
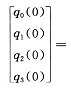 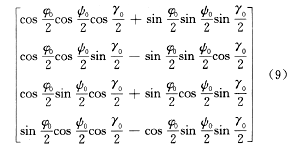
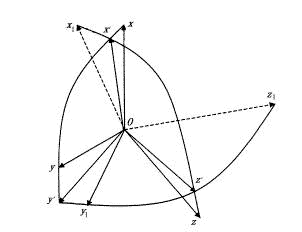
图2 坐标变换关系图
3.5 姿态角解算
由于由箭体坐标系到惯性坐标系的方向余弦矩阵如下:

由式(5)与式(10)比较可得
??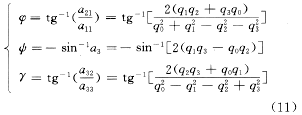 ?И? ?И?
4 激光陀螺捷联显式制导方案
4.1 制导方程
捷联显式制导方程包括导航方程、关机方程和导引方程。
4.1.1 导航方程
由图1可知,3个扰性加速度计测出沿箭体轴的3个视加速度分量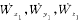 ?? ,则由式(7)解算出四元数q后,即可根据式(5)求出在惯性系的视加速度 ?? ,则由式(7)解算出四元数q后,即可根据式(5)求出在惯性系的视加速度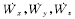 ,即 ,即
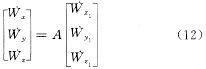
则由火箭的运动方程
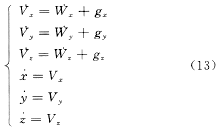
可得箭体的实时位置和速度的差分方程解如下:
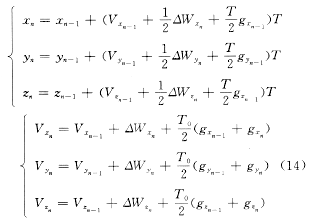
式中gx,gy,gx为考虑J2项摄动的重力项在惯性坐标系3个方向上的分量,具体表达式从略。
4.1.2 关机方程
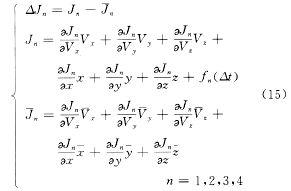
当ΔJn?变号时?火箭各级发动机关机。
式中 fn(Δt)为时间补偿函数;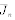 为标准关机特征量; 为标准关机特征量;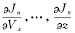 为标准弹道各级关机时刻的偏导数。 为标准弹道各级关机时刻的偏导数。
4.1.3 导引方程
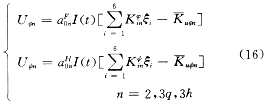
式中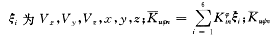 为阶梯函数,具体从略。 为阶梯函数,具体从略。
4.2 激光陀螺及加速度计的误差模型
4.2.1 捷联系统激光陀螺的误差模型
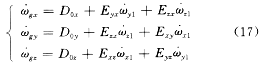
式中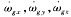 为陀螺产生的沿箭体坐标轴的静态误差;D0x,D0y,D0z为沿箭体轴的零位漂移系数;Eij为安装误差角。 为陀螺产生的沿箭体坐标轴的静态误差;D0x,D0y,D0z为沿箭体轴的零位漂移系数;Eij为安装误差角。
激光陀螺的测量误差只有与过载无关的漂移系数,且其稳定度高,经过误差补偿后,只剩下随机漂移。
4.2.2 石英加速度计的误差模型
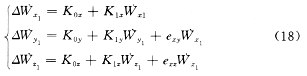
式中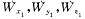 ,为沿各坐标的视加速度误差; ,为沿各坐标的视加速度误差;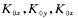 为零位误差系数; 为零位误差系数;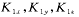 为比例系数误差;exy,exz为加速度表安装误差角。 为比例系数误差;exy,exz为加速度表安装误差角。
5 数值仿真
由于进行的是纯数值仿真,无陀螺输出信号可利用,故本文数值仿真是用平台计算机方案求出的姿态角增量作为陀螺输出的角增量信号的,由于克雷洛夫角的角速率与沿箭体轴的角速率有如下关系:
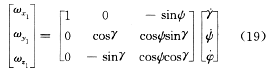
而
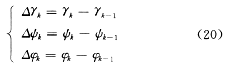
故
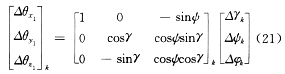
利用式(7)解算出四元数q0,q1,q2,q3,按式(5)求出转换矩阵A,再由式(11)求出姿态角,随后求出等效舵偏角δφ,δψ,δγ,再求出有关推力、阻力、重力、干扰力等,解算导航方程、关机方程、导引方程,并计算有关激光陀螺、加速度计误差引起的轨道入轨偏差。
5.1 方法误差
制导方程改为显式后,关机方程系数及导引方程系数不变,数值仿真表明,方法误差几乎无变化,其中,
Δa=0.453 ??km??;Δe=0.002 816;Δi=0.045 7°
5.2 工具误差
制导方程改为显示形式后,关机方程系数及导引方程系数不变,数值仿真表明,工具误差也几乎无变化。取计算步长为10 ms,用第4节的捷联惯性器件误差模型计算各项工具误差有如下结果:
a) a) 不考虑加速度计安装误差,激光陀螺和加速度计综合入轨误差为:
Δa=2.163km,Δe=0.000 264,Δi=0.012 45°;
b) b) 考虑加速度计安装误差,激光陀螺和加速度计综合入轨误差为:
Δa=11.379 km,Δe=0.001 886,Δi=0.106 2 °。
6 结 论
通过以上的研究和仿真计算可知,激光陀螺速率捷联显式制导方案中,用四元数二阶差分方程进行四元数解算,取数学平台计算步长为10 ms,制导计算精度已能满足。采用显式制导方程后,对方法误差及工具误差均无明显影响,其制导综合误差在加速度计安装误差补偿掉时为:
Δa=2.210 km,Δe=0.002 828,Δi=0.047 4 °
参 考 文 献
1 杨树林.激光陀螺与微机处理机联机试验.航天控制,1986.??
2 王永平.飞行器状态方程的实时解.航天控制,1985(1).??
3 范强.多头分导的显式制导方程.航天控制,1986(4).
|